Estatística Básica
Carregando, aguarde alguns segundos.

3 - Séries Estatísticas

Denomina-se série estatística toda tabela que apresenta a distribuição de um conjunto de dados estatísticos em função da época, do local ou da espécie (fenômeno).

3.1 - Tabelas

A apresentação tabular - tabela - é uma apresentação numérica que consiste em dispor os dados em linhas e colunas distribuídas de modo ordenado, segundo algumas regras práticas definidas pelo Conselho Nacional de Estatística e pelo IBGE.

As tabelas apresentam a vantagem de conseguir expor, sinteticamente em um só local, os resultados sobre determinado assunto, de forma a se obter uma visão global mais rápida do que se pretende analisar.

A integração de valores contidos nas tabelas favorece a utilização de representações gráficas, geralmente, uma maneira mais útil e elegante de demonstrar as características que serão analisadas.

Tabela é um quadro que resume um conjunto de observações.

Uma tabela compõe-se de:

  • Corpo: conjunto de linhas e colunas que contêm informações sobre a variável em estudo.
  • Cabecalho: parte superior da tabela que especifica o conteúdo das colunas.
  • Rodapé: parte inferior da tabela que especifica o conteúdo das linhas.
  • Coluna indicadora: parte da tabela que especifica o conteúdo das linhas.
  • Linhas: retas imaginárias que facilitam a leitura, no sentido horizontal, de dados que se inscrevem nos seus cruzamentos com as colunas.
  • Casa ou célula: espaço destinado a um só número.
  • Título: conjunto de informações, as mais completas possíveis, respondendo às perguntas: O quê? Quando? Onde? localizado no topo da tabela.

Exemplo:

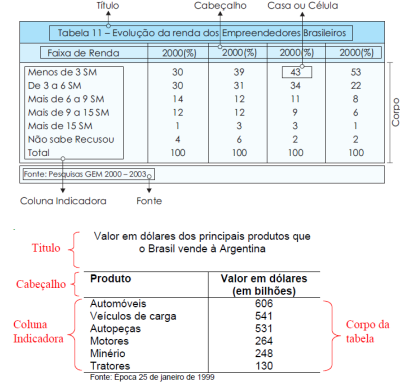
Devem-se considerar ainda os elementos complementares da tabela: fonte, chamadas e notas, colocadas, de preferência, no seu rodapé.

  • Fonte: indicação da entidade responsável pelo fornecimento dos dados.
  • Notas: são usadas para conceituação ou esclarecimento em geral.
  • Chamadas: são usadas para esclarecer certas minúcias em relação a casas, linhas e colunas. De acordo com a Resolução 886 da Fundação IBGE, nas casas ou células devemos colocar um traço horizontal (-) quando o valor é zero, não só quanto à natureza das coisas, como quanto ao resultado do inquérito. três pontos (...) quando não temos os dados.
  • Ponto de interrogação (?): quando temos dúvida quanto à exatidão de determinado valor.
  • Zero (0): quando o valor é muito pequeno para ser expresso pela unidade utilizada. Se os valores são expressos em numerais decimais, precisamos acrescentar à parte decimal um número correspondente de zeros (0,0; 0,00; 0,000; ...)

3.1.1 - Recomendações para a construção de tabelas

Na construção de tabelas, os dados são apresentados em colunas verticais e linhas horizontais, conforme a classificação dos resultados da pesquisa.

  • A tabela deve ser simples, pois tabelas simples são mais claras e objetivas. Desse modo, é conveniente que grandes volumes de informação sejam descritos em várias tabelas, em vez de em uma só.
  • A tabela deve ser autoexplicativa, ou seja, sua explicação deve estar desvinculada do texto.
  • Nenhuma casa da tabela deve ficar em branco, contendo sempre um número ou um sinal.
  • Se houver duas ou mais tabelas em um texto, deverão receber um número, que será referido no texto.
  • As colunas externas de uma tabela não devem ser fechadas.
  • Nas partes superior e inferior, as tabelas devem ser fechadas por linhas horizontais. O emprego de linhas verticais para a separação de colunas no corpo da tabela é opcional.
  • É conveniente que sejam evitados os arredondamentos. Quando for necessário o arredondamento dos números que compõem a tabela deve ser efetuado segundo critérios de minimização de erros. Com isso procura-se evitar o acúmulo de erros de arredondamentos decorrentes do processo de aproximação.
  • Deverá ser mantida uniformidade quanto ao número de casas decimais.
  • Os totais e subtotais devem ser destacados.
  • A tabela deve ser maior no sentido vertical que no horizontal. Entretanto, se uma tabela apresentar muitas linhas e poucas colunas (estreita demais), convém separá-la em uma maior quantidade de colunas. Nesse caso, as colunas deverão ser separadas por linhas duplas.

3.2 - Séries Estatísticas

Em uma série estatística observamos a existência de três elementos ou fatores: o tempo, o espaço e a espécie.

Conforme varie um dos elementos da série, podemos classificá-la em histórica (ou temporal), geográfica e específica.

As séries estatísticas consistem na apresentação das informações (variáveis estatísticas) em forma de tabelas, objetivando sintetizar os dados estatísticos observados e tornando-os mais compreensivos.

Uma tabela e mesmo um gráfico deve apresentar o cabeçalho com título, o corpo e o rodapé.

O cabeçalho com título deve conter o suficiente para compreender os seguintes elementos fundamentais:

  • Fato: fenômeno observado.
  • Espaço geográfico: local ou região onde o fato ocorreu.
  • Época: refere-se à data ou ao tempo em que o fato foi observado.

O corpo é reservado para o registro dos dados.

O rodapé é reservado para a identificação da fonte de dados.

3.2.1 - Série Histórica, Temporal, Evolutiva ou Cronológica

É a série estatística cujos dados são observados segundo a época de ocorrência.

O tempo é variável; o fato e o local são fixos.

Descreve os valores da variável, em determinado local, discriminados segundo intervalos de tempo variáveis.

Denomina-se série estatística toda tabela que apresenta a distribuição de um conjunto de dados estatísticos em função da época, do local ou da espécie (fenômeno).

Exemplo: produção agrícola na PB de 2004 a 2009

Ano produção (R$ 1.000.000)
2004 4,5
2005 5,3
2006 4,9
2007 5,1
2008 6,8
2009 7,1

3.2.2 - Série Geográfica, Espacial, Territorial ou de Localização

É a série estatística cujos dados são observados segundo a localidade de ocorrência.

O local varia; o tempo e o fato são fixos.

Descreve os valores da variável, em determinado instante, discriminados segundo regiões.

Exemplo: percentual do PIB destinado à educação por país.

Ano Percentual
EUA 2,5
Brasil 1,0
Japão 7,1
México 0,8

3.2.3 - Série Específica ou Categórica

É a série estatística cujos dados são agrupados segundo a modalidade de ocorrência.

Fato variável, tempo e local fixos.

Descreve os valores da variável, em determinado tempo e local, discriminados segundo especificações ou categorias.

Exemplo: PIB por setor econômico no Brasil em 2009

Setor PIB (US$ 1.000.000)
Primário 12,5
Secundário 5,8
Terceário 279,1

3.2.4 - Série Mista ou Conjugada – Tabela de Dupla Entrada

É uma combinação de duas ou mais dos 3 tipos de séries anteriores.

Muitas vezes temos necessidade de apresentar, em uma única tabela, a variação de valores de mais de uma variável, isto é, fazer uma conjugação de duas ou mais séries.

Conjugando duas séries em uma única tabela, obtemos uma tabela de dupla entrada.

Em uma tabela desse tipo ficam criadas duas ordens de classificação: uma horizontal (linha) e uma vertical (coluna).

Exemplo: produção agrícola dos principais produtos, por região no Brasil, em 2009, com valores em milhões de toneladas.

Região Grão Frutas Legumes Outros Total
Norte 1,5 45,2 5,4 0,5 52,6
Nordeste 2,4 120,0 1,2 4,5 128,1
Centro-Oeste 10,5 10,5 4,2 1,5 26,7
Sudeste 50,7 100,1 10,2 5,9 166,9
Sul 12,5 75,0 15,2 5,2 107,9

3.3 - Dados Absolutos e Dados Relativos

No estudo sobre formas de apresentação de dados estatísticos, principalmente quando se planeja proceder a uma análise exploratória ou descritiva para uma variável, será apontado que em muitos casos pode ser mais conveniente a apresentação de resultados na forma relativa ao invés de na forma absoluta.

3.3.1 - Dados Absolutos

Os dados estatísticos resultantes da coleta direta da fonte, sem outra manipulação senão a contagem ou medida, são chamados dados absolutos.

Por exemplo, se dissermos “uma sala possui 20 alunos”, esses dados são considerados absolutos.

A leitura dos dados absolutos é sempre enfadonha e inexpressiva, embora esses dados traduzam um resultado exato e fiel, não têm a virtude de ressaltar de imediato as suas conclusões numéricas.

Daí o uso imprescindível que faz a Estatística dos dados relativos.

3.3.2 - Dados Relativos

Dados relativos: resultado de comparações por quocientes (razões) que se estabelecem entre dados absolutos, e têm por finalidade realçar ou facilitar as comparações entre quantidades.

Traduzem-se os dados relativos, em geral, por meio de porcentagens, índices, coeficientes e taxas.

3.3.2.1 - Porcentagens

O emprego da porcentagem é de grande valia quando queremos destacar a participação da parte no todo.

Formalmente, PORCENTAGEM é uma RAZÃO cujo CONSEQUENTE (DENOMINADOR) é 100.

Se p = porcentagem, P é o valor da Parte e B é o valor do todo (ou Base), então pela definição:

$\frac{p}{100}$ = $\frac{P}{B}$

Exemplo: série com as matrículas nas escolas da cidade A.

Categoria Número de alunos
Ensino Fundamental 19286
Ensino Médio 1681
Ensino Superior 234
Total 21201

Calculemos as porcentagens dos alunos de cada nível.

Categoria Cálculo Resultado Percentual
Ensino Fundamental $\frac{19286 x 100}{21201}$ 90,98% 91,0%
Ensino Médio $\frac{1681 x 100}{21201}$ 7,92 7,9%
Ensino Superior $\frac{234 x 100}{21201}$ 1,10 1,1%

Com esses dados, podemos formar uma nova coluna na série em estudo: percentual.

Exemplo: Matrícula nas escolas da cidade A com percentual.

Categoria Número de alunos Percentual
Ensino Fundamental 19286 91,0%
Ensino Médio 1681 7,9%
Ensino Superior 234 1,1%
Total 21201 100,0%

Os valores dessa nova coluna nos dizem que, de cada 100 alunos da cidade A, 91 estão matriculados no Ensino Fundamental; 8, aproximadamente, no Ensino Médio e 1 no Ensino Superior.

O emprego da porcentagem é de grande valia quando é nosso intuito destacar a participação da parte no todo.

Consideremos, agora, as séries com as matrículas nas escolas das cidades A e B.

Categoria Cidade A Cidade B
Ensino Fundamental 19286 38660
Ensino Médio 1681 3399
Ensino Superior 234 424
Total 21201 42483

Qual das cidades tem, comparativamente, maior número de alunos em cada nível?

Como o número total de alunos é diferente nas duas cidades, não é fácil concluir a respeito usando os dados absolutos.

Porém, usando as porcentagens, tal tarefa fica bastante facilitada.

Assim, acrescentando, na tabela anterior, as colunas correspondentes às porcentagens, obtemos as matrículas nas escolas das cidades A e B com percentuais.

Categoria Cidade A Percentual Cidade B Percentual
Ensino Fundamental 19286 91,0 38660 91,0
Ensino Médio 1681 7,9 3399 8,0
Ensino Superior 234 1,1 424 1,0
Total 21201 100,0 42483 100,0

O que nos permite dizer que, comparativamente, contam, praticamente, com o mesmo número percentual de alunos em cada nível.

Observações:

  • Do mesmo modo que tomamos 100 para base de comparação, também podemos tomar outro número qualquer, entre os quais destacamos o número 1. É claro que, supondo o total igual a 1, os dados relativos das parcelas serão menores que 1.
  • Em geral, quando usamos 100 para base, os dados são arredondados até a primeira casa decimal, e quando tomamos 1 por base, são arredondados até a terceira casa decimal.

3.3.2.2 - Os índices. Índices Econômicos.

Os índices são razões entre duas grandezas tais que uma não inclui a outra.

São exemplos de índices:

  • indice-encefalico = $\frac{\text{diametro-transverso-cranio}}{\text{diametro-longitudinal-cranio}} \times 100$
  • quociente-intelectual = $\frac{\text{idade-mental}}{\text{idade-cronologica}} \times 100$
  • densidade-demografica = $\frac{\text{populacao}}{\text{superficie}}$

Índices Econômicos:

  • producao-per-capita = $\frac{\text{valor-producao}}{\text{populacao}}$
  • consumo-per-capita = $\frac{\text{consumo-bem}}{\text{populacao}}$
  • renda per capita = $\frac{\text{renda}}{\text{populacao}}$
  • receita per capita = $\frac{\text{receita}}{\text{populacao}}$

3.3.2.3 - Coeficientes

Os coeficientes são razões entre o número de ocorrências e o número total (número de ocorrências e número de não ocorrências).

São exemplos de coeficientes:

  • natalidade=$\frac{\text{nascimentos}}{\text{populacao-total}}$
  • receita-per-capita=$\frac{\text{receita}}{\text{populacao}}$

Coeficientes Educacionais:

  • evasao-escolar=$\frac{\text{alunos evadidos}}{\text{matriculas}}$
  • aproveitamento-escolar=$\frac{\text{alunos-aprovados}}{\text{matriculas}}$
  • recuperacao-escolar=$\frac{\text{alunos-recuperados}}{\text{recuperacao}}$

3.3.2.4 - Taxas

As taxas são coeficientes multiplicados por uma potência de 10 (10, 100, 1000, etc.) para tornar o resultado mais inteligível.

São exemplos de taxas:

  • Taxa de mortalidade = coeficiente de mortalidade x 1000
  • Taxa de natalidade = coeficiente de natalidade x 1000
  • Taxa de evasão escolar = coeficiente de evasão escolar x 100

Exemplo:

O Estado A apresentou 733.986 matrículas na 1ª série, no início do ano de 2017, e 683.816 no fim do ano.

O Estado B apresentou, respectivamente, 436.127 e 412.457 matrículas.

Qual é o Estado que apresentou maior evasão escolar?

Resposta:

O Estado que apresentou maior evasão escolar foi o Estado A:

  • A → taxa-evasao = $100 \times \frac{\text{733.986 - 683.816}}{733.986}$ = 0,0683 x 100 = 6,83 = 6,8%
  • B → taxa-evasao = $100 \times \frac{\text{436.127 - 412.457}}{436.127}$ = 0,0542 x 100 = 5,42 = 5,4%
Arduino
Coautor
Betobyte
Autor
Autores
||| Áreas ||| Estatística ||| Python ||| Projetos ||| Dicas & Truques ||| Quantum ||| Estatística Básica || Estatística Básica || Estatistica Avançada || Bayes || Aulas | Conceitos Fundamentais (Conceitos fundamentais e compreensão da estatística, tratando da coleta, da análise, da interpretação e da apresentação de massas de dados numéricos, também significando um conjunto de dados numéricos.) | População e Amostra (População e amostra como um conjuntos de objetos, itens ou eventos com alguma característica ou propriedade comum mensurável, ordenável ou comparável de acordo com os limites propostos e objetivos do estudo.) | Séries Estatísticas (Séries estatísticas como distribuição de conjuntos de dados estatísticos em função da época, do local ou da espécie (fenômeno).) | Gráficos Estatísticos (Representação gráfica estabelecendo correspondência entre os termos da série e determinada figura geométrica, de tal modo que cada elemento da série seja representado por uma figura proporcional.) | Distribuição de Frequência (Distribuição de Frequência como conjunto de dados em uma tabela conforme as frequências ou repartições de seus valores, podendo ser discreta ou contínua de uma série estatística em que permanecem constantes o fato, o local e a época em que o fenômeno ocorreu.) | Medidas de Posição (Medidas de posição com a localização da maior concentração de valores de uma distribuição, isto é, se ela se localiza no início, no meio ou no final, ou, ainda, se há uma distribuição por igual.) | Medidas de Dispersão (Medidas de dispersão ou variabilidade empregadas na descoberta do grau de variabilidade ou dispersão dos valores observados em torno da média aritmética, medindo a representatividade da média e destacam o nível de homogeneidade ou heterogeneidade dentro de cada grupo estatístico analisado.) | Medidas de Assimetria/Curtose (Medidas de forma por descreverem a forma da curva de distribuição dos dados, indicando o grau de assimetria de uma distribuição de frequências unimodal em relação a uma linha vertical que passa por seu ponto mais elevado ou o grau de achatamento de uma distribuição em relação a distribuição padrão denominada curva normal.) | Probabilidade (O cálculo de probabilidades é uma necessidade essencial para o estudo de Estatística Indutiva (ou Inferencial) pelo fato de a maioria dos fenômenos tratados na Estatística serem de natureza aleatória ou probabilística.) | Distribuição Binomial (A probabilidade de ocorrerem k sucessos e (n–k) fracassos dada pelo termo geral do Binômio de Newton.) |